
STATISTIKA A FINANČNÍ MATEMATIKA
Jednoduché úročení polhůtní
Při tomto úročení se úročí pouze základní jistina (kapitál), úroky se vyplácejí po skončení úrokového období a k základní jistině se nepřipočítavájí. Úrok se obvykle počítá podle vzorce:
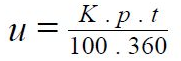
Legenda:
u úrok
K peněžní částka (kapitál)
p roční úroková sazba v procentech
t doba splatnosti kapitálu ve dnech
Rok se obvykle počítá jako 360 (t je obvykle z intervalu 1 až 359).
Pokud vyjádříme úrokovou sazbu jako desetinné číslo a splatnost v letech, může použít následující vzorec:
u = K . n
Legenda:
i = p / 100 úroková sazba vyjádřená jako desetinné číslo
n = t /360 doba splatnosti v letech
Pro výpočet n vzniklo několik standardů. Pro určení t (doba splatnosti ve dnech) se užívá:
- ACT - skutečný počet dní, přičemž první den se nepočítá
- 30E - celé měsíce se vždy počítají bez ohledu na skutečný počet dní v měsící po 30 dnech
- 30A - může se od 30E lišit o jeden den, pokud konec období připadl na 31. den v měsíci a současně počátek nikoli na 30. nebo 31. den v měsíci.
Jakožto počet dní v roce se zpravidla uvažuje 360, lze však pracovat i 365 dny (resp. s 366 dny v přestupném roce). Na základě této skutečnosti vznikly další kombinované standardy. Dále jsou uvedeny nejběžnější z nich:
- ACT/365 - anglická metoda
- ACT/360 - francouzská metoda
- 30E/360 - německá či obhodní metoda.
Užití jednoduchého úročení
Jednoduché úročení se používá v případě období kratšího než jeden rok, pokud se úroky připisují ročně. Dále se užívá při eskontu směnek.
Kalkulačka jednoduchého úročení
Zdroj: Pavel Mička, algoritmy.net, kód podléhá MIT licenci
Příklady:
Př. 1 - Vzorový příklad: Kolik bude činit hodnota jistiny 5 000 Kč po třech letech, bude-li úročena 6 % jednoduchým úročením?
Postup a výsledek: Jako vklad zadáme 5000, úrokovou míru 0.06 (pozor - desetinná tečka, nikoli čárka) a počet období 3. Výsledek: 5 900 Kč.
Př. 2: Kolik bude činit hodnota jistiny 115 000 Kč po jednom roce úročení 3 %?
Př. 3: Kolik bude činit hodnota jistiny 450 000 Kč po pěti letech úročení 8 %?